План
1. Геометрическая прогрессия 5. Функция и её свойства
2. Геометрия 6. Теорема Пифагора
3. Правильные многогранники
4. Шпаргалка по тригонометрии
Геометрическая прогрессия
Геометрическая прогрессия играет большую и важную роль не только в школьном курсе алгебры, но и (как я мог убедится) в дальнейшем обучении в высших учебных заведениях. Важность этого на первый взгляд небольшого раздела школьного курса заключается в его чрезвычайно широких областях применения, в частности он часто применяется в теории рядов, рассматриваемой на
II-III курсах университета. Поэтому мне кажется крайне важным дать здесь полное описание этого курса, дабы внимательный читатель мог повторить уже известный ему (надеюсь - прим. автора) из школьного курса материал, или даже почерпнуть много нового и интересного.Прежде всего необходимо дать определение геометрической прогрессии, ибо не определившись о предмете разговора невозможно продолжать сам разговор. Итак: числовая последовательность, первый член которой отличен от нуля, а каждый член, начиная со второго, равен предшествующему члену, умноженному на одно и тоже не равное нулю число, называется геометрической прогрессией
.Внесу некоторую ясность в данное выше определение: во-первых, мы требуем от первого члена неравенства нулю для того, что при умножении его на любое число мы в результате снова получим ноль, для третьего члена опять ноль, и так далее. Получается последовательность нулей, которая не попадает под данное выше определение геометрической прогрессии и не будет являться предметом нашего дальнейшего рассмотрения.
Во-вторых, число на которое умножаются члены прогрессии опять же не должно быть равно нулю, по вышеизложенным причинам.
В-третьих, предоставляю возможность вдумчивому читателю самому найти ответ на вопрос, почему мы умножаем все члены прогрессии на одно и тоже число, а не, скажем, на разные. Ответ не так прост, как может показаться вначале.
Далее, из определения геометрической прогрессии следует, что отношение любого ее члена к предшествующему равно одному и тому же числу, т. е.
b2:b1 = b3:b2 = ... = bn:bn-1 = bn+1:bn = ... . Это число называется знаменателем геометрической прогрессии и обычно обозначается буквой q.Несколько слов необходимо сказать и о способах задания геометрической прогрессии. Для того чтобы задать геометрическую прогрессию (
bn), достаточно знать ее первый член b1 и знаменатель q. Например, условиями b1 = 2, q = -5 (q < 0) задается геометрическая прогрессия 2, -10, 50, -250, ... . Эта прогрессия не является ни возрастающей ни убывающей последовательностью.Следует заметить, что: последовательность называется возрастающей (убывающей) если каждый последующий член последовательности больше (меньше) предыдущего
.Таким образом, если
q > 0 (qОднако, если
q = 1, то все члены прогрессии равны между собой. В этом случае прогрессия является постоянной последовательностью.Любая геометрическая прогрессия обладает определенным характеристическим свойством. Это свойство является следствием самого правила задания геометрической прогрессии: последовательность
(bn) является геометрической прогрессией тогда и только тогда, когда каждый ее член, начиная со второго, есть среднее геометрическое соседних с ним членов, т. е.![]() .
.
Пользуясь этим свойством можно находить любой член геометрической прогрессии если известны два рядом стоящие.
Для нахождения
n-ного члена геометрической прогрессии есть еще одна формула. Для того чтобы найти любой член геометрической прогрессии необходимо, чтобы она была задана, т. е. были известны значения b1 и q:![]() .
.
Так как геометрическая прогрессия это числовая последовательность, то мы можем найти ее сумму. Для нахождения суммы геометрической прогрессии применяют следующую формулу:

Если в данную формулу подставить вместо
bn его выражение в виде b1qn-1, то получим еще одну формулу для вычисления суммы геометрической прогрессии:
У геометрической прогрессии есть еще одно свойство, а именно: из определения знаменателя геометрической прогрессии следует, что
b1bn = b2bn-1 = ..., т. е. произведение членов, равно отстоящих от концов прогрессии, есть величина постоянная. Наконец, нельзя не коснуться такого важного с научной точки зрения понятия, как бесконечной геометрической прогрессии приНайти эту сумму можно по следующей формуле:
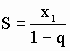
Заканчивая описание геометрической прогрессии хочется лишний раз повторить, что за видимой простотой геометрической прогрессии скрывается большой прикладной потенциал этого раздела алгебры.
Геометрия
Понятие о центре тяжести было впервые изучено примерно 2200 лет назад греческим геометром Архимедом, величайшим математиком древности. С тех пор это понятие стало одним из важнейших в механике, а также позволило сравнительно просто решать некоторые геометрические задачи.
Именно приложение к геометрии мы и будем рассматривать. Для этого нужно ввести некоторые определения и понятия. Под материальной точкой понимают точку, снабжённую массой. Для наглядности можно себе физически представить материальную точку в виде маленького тяжёлого шарика, размерами которого можно пренебречь. В связи с этим будем часто указывать только числовое значение той или иной физической величины, но не будем отмечать её наименование, считая, что оно само собой подразумевается. Например, выражение: «В D ABC сторона BC равна a, а в вершине A мы помещаем массу a» означает: «Длина стороны BC равна a ñàíòèìåòðàì, à ìàññà, ïîìåù¸ííàя в вершине A, равна a грамм».
Если в точке A помещена масса m, то образующуюся материальную точку будем обозначать так: (A, m). Иногда, когда это не может вызвать недоразумений, мы будем её обозначать одной буквой A. Массу m иногда называют «нагрузкой точки A».
Центром тяжести двух материальных точек (A, a) и (B, b) называется такая третья точка C, которая лежит на отрезке AB и удовлетворяет «правилу рычага»: произведение её расстояния CA от точки А на массу а равно произведению её расстоянию СВ от точки В на массу b; таким образом,
![]() .
.
Это равенство можно записать и так:
 ,
,
то есть расстояние от центра тяжести двух материальных точек до этих точек обратно пропорциональны массам, помещённым в этих точках. Центр тяжести будет ближе к точке с большей массой. Из определения следует: если прямая проходит через центр тяжести двух материальных точек и через одну из них, то она пройдёт и через другую.
Центр тяжести двух материальных точек имеет весьма простой механический смысл. Представим себе жёсткий «невесомый» стержень АВ, в концах которого помещены массы а и b (рис. 1). «Невесомость» стержня практически означает, что его масса по сравнению с массами a и b настолько незначительна, что ею можно пренебречь. Центр тяжести С материальных точек (A, a) и (B, b) — это такая точка, в которой надо подпереть стержень AB, чтобы он был в равновесии.
|
рис. 2 |
Для дальнейшего полезно также ввести понятие «объединение» или равнодействующей двух материальных точек. Под этим мы будем понимать материальную точку, которая получится, если в центре тяжести двух материальных точек поместить массы обеих точек.
|
D
рис. 1 |
Пример.
Пусть в концах невесомого тонкого стержня
AB
(рис. 2), длина которого равна 20 ед. Помещены такие массы: в
A
— 6 ед., в
B — 2
ед. Центром тяжести материальных точек (A,
6) и (B,
2) будет точка
C,
лежащая на стержне
AB,
определяемая условием: 6CA=2CB,
или CB=3CA.
Поэтому АВ=CB+CA=4AC.
Отсюда
 (ед.).
Объединение материальных точек (A,
6) и
(B,2)
будет материальная точка (С, 8).
(ед.).
Объединение материальных точек (A,
6) и
(B,2)
будет материальная точка (С, 8).
Центр тяжести трёх материальных точек находится следующим образом: находят объединение двух из этих материальных точек и затем ищут центр тяжести образовавшейся таким образом четвёртой материальной точки и третей из данных материальных точек.
Вообще, центр тяжести n материальных точек при n>2 находится так: надо сначала найти центр тяжести n-1 материальных точек, поместить в этой точке массы всех n-1 точек, затем найти центр тяжести этой вновь образовавшейся материальной точки с n-й материальной точкой.
Если поместить в центре тяжести несколько материальных точек массы всех этих точек, то образующуюся таким образом новую материальную точку назовём объединением данных материальных точек.
Для решения задач важны следующие простейшие свойства центров тяжести.
I. Положение центра тяжести n материальных точек не зависит от порядка, в котором последовательно объединяются эти точки. (Теорема о единственности центра тяжести для системы из n материальных точек.)
II. Положение центра тяжести системы из n материальных точек не изменится, если заменить несколько материальных точек их объединением. (Теорема о возможности группировки материальных точек.)
При рассмотрении некоторых вопросов механики оказывается выгодным ввести понятие статического момента.
Пусть имеется некоторая точка C и, кроме того, материальная точка Aº(A, m). Статическим моментом материальной точки А относительно точки С мы назовём произведение m×CA и будем его кратко обозначать так: МомСА.
Пользуясь понятием статического момента, определение центра тяжести можно сформулировать так: точка С называется центром тяжести двух материальных точек Aº(A, m1) и Bº(B, m2), если С лежит на отрезке АВ и МомСА=МомСB.
Пусть теперь на некотором луче с началом S (рис. 3) расположена система из некоторых n материальных точек
A1º(A1, m1), A2º(A2, m2), …, Anº(An, mn).
|
рис. 3 |
Статическим моментом этой системы относительно начала луча S называют сумму моментов всех точек системы относительно начала луча,
т.е. сумму K=МомSA1+ МомSA2+ МомSA3+…+ МомSAn или, подробнее,
K=m1×SA1+ m2×SA2+ m3×SA3+…+ mn×San.
Пример. Если система состоит из трёх точек (A1, 1), (A2, 4), (A3, 9) и SA1=1, SA2=2, SA3=3 (рис. 4), то статический момент системы равен
K=1×1 + 4×2 + 9×3 = 36.
Понятно, что в системе SGC момент будет иметь размерность г×см. Но мы ранее договорились, что размерность будем каждый раз подразумевать, но нигде не указывать.
|
S A1 А2 A3
рис. 4 |
В наших рассуждениях основными объектами были «материальные точки». С точки зрения математики материальная точка — это комплекс, состоящий из геометрической точки и некоторого (положительного) числа.
В математике не раз приходится сталкиваться с таким явлением: комплекс из двух каких-то математических объектов рассматривают как некоторый новый объект, который затем уже подвергается специальному изучению. Так, например, в курсе алгебры вводится понятие комплексного числа как комплекса (пары) двух действительных чисел.
В строгих курсах геометрии таким образом вводится, например, понятие отрезка как комплекса (пары) двух точек; понятие угла может быть введено сходным образом: угол можно рассматривать как комплекс двух лучей с общим началом.
Если имеется у нас какая-либо материальная точка Аº(A, m), то мы (геометрическую) точку A будем иногда называть носителем или аффиксом этой материальной точки, а число m будем по-прежнему называть массой этой материальной точки.
Равенству вида (A, a)º(B, b) мы придаём такой смысл: две материальные точки имеют один и тот же носитель (AºB) и равные массы (aºb).
Решение почти всех ранее рассмотренных задач опиралось на то, что мы «объединяли некоторые материальные точки в их центре тяжести»; точнее, заменяли некоторые материальные точки их объединением. При этом под объединением двух материальных точек (A, a) и (B, b) мы понимали некоторую новую материальную точку (С, a+b), где С — центр тяжести двух данных материальных точек. Можно было бы так сказать: объединением двух материальных точек называется такая новая материальная точка, носителем которой является центр тяжести данных материальных точек и масса которых равна сумме масс этих материальных точек.
Вместо «объединения» можно употреблять выражение «сумма».
Если материальная точка Сº(С, с) является объединением двух других материальных точек Aº(A, a) и Bº(B, b), то мы будем это записывать так:
(A, a) + (B, b) = (C, c)
или, короче,
A + B = C.
Мы не будем исключать и тот случай, когда две материальные точки имеют один и тот же носитель. В этом случае, естественно, будем считать носителем объединения их общий носитель. Таким образом, (А, а) + (А, b) = (A, a+b).
У нас возникает своеобразное исчисление, своеобразная алгебра. В этой алгебре имеет место переместительный закон: A + B = B + A. Это следует из самого определения центра тяжести двух материальных точек. Имеет место также сочетательный закон:
(A1 + A2) + A3 = A1 + (A2 + A3),
или, иначе,
[(A1, m1) + (A2, m2)] + (A3, m3) = (A1, m1) + [(A2, m2) + (A3, m3)].
Подробнее: Найдём ли мы сначала объединение A12 двух материальных точек А1 и А2 и затем найдём объединение этой материальной точки А12 с третьей материальной точкой А3, или сначала найдём объединение А23 материальных точек А2 и А3, а затем найдём объединение материальных точек А1 и А23, в обоих случаях мы придём к одному и тому же результату, к одной и той же материальной точке.
Понятно, что смысл этого утверждения состоит в том, что центр тяжести трёх материальных точек не зависит от порядка, в котором объединяются эти точки.
В наших рассуждениях «материальная точка» (A, m) выступала как комплекс, состоящий из некоторой геометрической точки А и некоторого положительного числа т. Это число т мы до сих пор называли массой. Однако его можно было бы назвать и каким-либо другим словом, скажем, «весом». Все наши предыдущие рассуждения останутся, конечно, в силе, если заменить слово «масса» словом «вес». Мы бы в таком случае уже не говорили, например, «рассмотрим материальную точку (А, т) с массой т», а сказали бы: « рассмотрим материальную точку (А, т) с весом т».
До сих пор мы наглядно представляли материальную точку (А, т) в виде материального шарика, размерами которого можно пренебречь, имеющего массу т. Но с таким же успехом мы могли бы наглядно представить ту же материальную точку в виде такого же шарика с весом т.
Мы далее рассматривали центр тяжести двух материальных точек вида (A, a) и (B, b) и определяли его по правилу рычага. Если мы хотим этот центр тяжести наглядно представить в виде центра тяжести двух шариков, помещённых в точках А и В и весящих соответственно а и b единиц, то нужно сделать несколько оговорок (которые, впрочем, само собой подразумеваются). Во всяком случае эти шарики должны быть на небольшом расстоянии друг от друга, настолько небольшом, чтобы можно было без чувствительной погрешности считать, что при свободном падении они будут перемещаться параллельно и с одним и тем же ускорением. Кроме того, если шарики из различных материалов, то важно, чтобы удельным весом газа или жидкости, заполняющей окружающую их среду, возможно было пренебречь. Такие условия практически будут соблюдены, например, если мы не выйдем за пределы, скажем, комнаты или даже города.
До сих пор, рассматривая материальную точку, то есть пару вида (А, т),мы всегда полагали, что её «масса» (или «вес») — положительное число. Для решения некоторых геометрических задач весьма полезно рассмотреть и такой случай, когда это число т может быть произвольным действительным числом. Такую пару мы, сохраняя старую терминологию, будем по-прежнему называть материальной точкой, а для числа т сохраним старое название «масса» (или «вес»). Как же себе наглядно представить «материальную точку» с отрицательной «массой»?
Приведём одну конкретную физическую картину, которая позволит читателю наглядно представить материальные точки с произвольными вещественными «массами».
Пусть имеется какой-то бассейн, заполненный водой. Пусть шарик, который висит в воздухе (точнее, в пустоте) р единиц (скажем, р грамм), помещён в какую-то точку А внутри этого бассейна.
Рассмотрим сначала случай, когда удельный вес шарика больше 1 (например, когда шарик железный). Понятно, что шарик пойдёт в этом случае ко дну. Если под водой взвесить этот шарик (скажем, с помощью пружинных весов), то весы покажут меньше, чем р единиц. Нетрудно, если будет необходимость, узнать, сколько будет весить шарик под водой. Пусть удельный вес шарика равен d, а объём V. Тогда V=p/d. Считая удельный вес воды равным 1, найдём что вес воды в объёме, занимаемом шариком, равен (p/d)×1=p/d. В силу закона Архимеда вес т шарика под водой (его «подводный вес») определяется по такой формуле:
![]() (*)
(*)
Понятно, что т — подводный вес шарика — это результирующая сила, которая получается от сложения двух сил, действующих на шарик: силы тяжести и выталкивающей силы воды.
Обратим внимание на то, что в рассматриваемом случае (при d>1) m>0 и эта сила направлена вниз. Пусть теперь удельный вес шарика меньше 1 (например, когда шарик сделан из пробки). В этом случае шарик будет выталкиваться из воды («вверх»). Результирующая сила m, под действием которой шарик будет выталкиваться вверх, будет в соответствии с законом Архимеда равна по-прежнему
![]() ,
,
но теперь это выражение отрицательно (ибо d<1) и, следовательно, сила направлена вверх.
Пусть, наконец, d=1, то есть удельный вес шарика равен удельному весу воды. Такой шарик можно себе представить изготовленным из дерева и содержащим металлическую сердцевину (причём металл и дерево должны, понятно, быть взяты во вполне определённом отношении). Можно его себе представить изготовленным также из специальной пластмассы. Его вес в воде по-прежнему определяется по (*), а так как d=1, то т=0, то есть такой шарик в воде невесом. При любом положении точки А в воде он останется в покое.
Таким образом, при любом d (d>0) выражение (*) характеризует величину результирующей силы, которая действует на шарик; она направлена «вниз» при т>0 (т.е. при d>1) и «вверх» при т<0 (т.е. при d<1). При т>0 мы эту силу назвали «подводным весом шарика». То же название мы сохраним и при т£0. Таким образом, подводный вес шарика может выражаться как положительным, так и отрицательным числом или нулём.
Перейдём теперь к наглядному истолкованию «материальных точек». Материальную точку (А, т) при любом т (положительном, отрицательном или равном нулю) мы можем наглядно представлять в виде шарика, размерами которого можно пренебречь, помещённого в точке А и имеющего подводный вес т.
Значит, то число т, которое мы условились называть «массой» материальной точки, мы истолковываем, как «подводный вес шарика». При т>0 мы материальную точку (А, т) наглядно представляем в виде шарика, тонущего в воде (например, железного). При т<0 соответственно, всплывающего на поверхность воды (например, пробкового), а при т=0 — из пластмассы — с таким же удельным весом, что и у воды. В воде он будет невесомым. Будучи помещён в какой-либо точке, он под действием силы тяжести и выталкивающей силы воды останется на месте.
Если будет идти речь о двух материальных точках, то мы их можем себе наглядно представлять нанизанными на тонком прямолинейном стержне, изготовленном из той же «невесомой» (в воде) пластмассы, о которой мы говорили выше. Ниже мы будем говорить о центре тяжести двух материальных точек. Практически этот центр тяжести можно наглядно представить как точку, в которой нужно подпереть или за которую нужно подвесить невесомый (в воде) стержень для того, чтобы он вместе с нанизанными на нём «материальными точками» оказался в безразличном равновесии.
Всегда ли найдётся такая точка на этом стержне между этими двумя «материальными точками»? Не может ли она оказаться вне отрезка, соединяющего данные материальные точки? Не может ли случиться, что такой точки вовсе нет? Это мы выясним ниже.
Аналогичным образом можно себе представить центр тяжести любого числа материальных точек.
Встречающееся ниже понятие «объединение нескольких материальных точек» можно наглядно истолковать как равнодействующую подводных весов всех тех шариков, которые наглядно изображают эти материальные точки.
Иногда полезно дать более широкое наглядное толкование понятия материальной точки с произвольной вещественной «массой».
|
рис. 5 |
Сделаем одно предварительное замечание. На каждой прямой мы можем выбрать положительное направление и единицу масштаба. Если это уже сделано, то прямую иногда называют осью.
Каждый отрезок (скажем, АВ) можно рассматривать как направленный, причём сначала мы называем начало отрезка (А), а затем — его конец (В); направление отрезка — от А к В. Если отрезок лежит на оси (или параллелен ей), то его направление может:
1) совпадать с направлением оси;
2) быть противоположным направлением оси.
В первом случае мы величиной отрезка называем его длину; во втором случае величиной отрезка мы называем его длину, взятую со знаком минус (-).
Таким образом, величина отрезка, лежащего на какой-нибудь оси, или параллельного оси — это его длина, взятая со знаком плюс или минус, в зависимости от того, будут ли направление отрезка и оси одинаковы или противоположны. Величину отрезка АВ будем обозначать так: АВ.
В нашем примере (рис. 5) АВ=3, DC= -2, ВА= -3. Вообще АВ= -ВА.
Вернёмся теперь к вопросу о возможном физическом истолковании материальных точек с произвольными вещественными массами.
Мы будем представлять, что в пространстве произвольным образом выбрана какая-либо ось l. Материальную точку (А, т) можно наглядно истолковать как силу, параллельную оси l и приложенную к точке А.
Число т («масса») характеризует абсолютную величину (или, как говорят иногда, «напряжение») и направление этой силы: сила и ось одинаково направлены, если т>0, и противоположно направлены, если т<0; по абсолютной величине сила равна ½т½ (единицам силы). Если т=0, то сила равна нулю. Материальную точку вида (А, 0) можно назвать «незагруженной точкой» или «нулевой силой».
|
С
рис. 6 |
Когда будем ниже говорить о «центре тяжести нескольких материальных точек», то его можно себе наглядно представлять как центр параллельных сил, а «объединение нескольких материальных точек» — как равнодействующую нескольких параллельных сил, приложенную в центре параллельных сил.
Для геометрических приложений важно, что почти всё основное, что мы говорили относительно материальных точек с положительными массами, возможно обобщить на случай материальных точек с произвольными вещественными массами.
Понятие центра тяжести двух материальных точек (с произвольными вещественными массами) можно ввести так.
Центром тяжести двух материальных точек (А, а) и (B, b) (рис. 6) называется такая точка С, лежащая на оси АВ (положительное направление от А к В), которая удовлетворяет условию: а×АС=b×СВ.
|
А
В
рис. 7 |
Центр тяжести С двух материальных точек (А, а) и (B, b) будет лежать между А и В, лишь если «массы» а и b одного знака. Если а и b разных знаков, то С вне отрезка АВ (рис. 7).
Лишь в одном случае центр тяжести материальных точек (А, а) и (B, b) с различными носителями (А¹В) не существует, — именно, когда массы их противоположны по знаку, но не равны по абсолютной величине (то есть, если а = -b ¹ 0). В связи с этим мы будем называть две материальные точки вида (А, а) и (В, -а) (А¹В, а¹0) механической парой.
Этот
случай можно себе представить как предельный для того случая, когда
а¹-b,
но а® -b.
Если а¹-b,
а¹0,
b¹0,
то можно написать
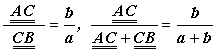 , т.е.
, т.е. 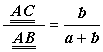 . Если а ®
-b,
то а +
b
® 0 и,
следовательно, АС ®
¥, то есть точка С
неограниченно удаляется вдоль прямой АВ. Поэтому
иногда говорят, что если
a = -b,
то центр тяжести двух материальных точек (А, а) и
(B, b)
«лежит в бесконечно удалённой точке прямой АВ».
. Если а ®
-b,
то а +
b
® 0 и,
следовательно, АС ®
¥, то есть точка С
неограниченно удаляется вдоль прямой АВ. Поэтому
иногда говорят, что если
a = -b,
то центр тяжести двух материальных точек (А, а) и
(B, b)
«лежит в бесконечно удалённой точке прямой АВ».
Оставаясь здесь в рамках элементарной геометрии, мы будем эту фразу рассматривать как образное выражение того, что центра тяжести в данном случае нет.
Если одна из двух материальных точек является незагруженной, а «масса» другой материальной точки отлична от нуля, то их центр тяжести совпадает с носителем загруженной точки. В связи с этим имеет смысл все незагруженные точки считать равными, то есть считать, что при любых А и В ( А, 0) ºº (В, 0).
Задача о нахождении центров тяжести двух незагруженных точек является неопределенной: существует бесконечно много точек, которые можно рассматривать в качестве центров тяжестей этих двух точек. Мы не будем останавливаться на рассмотрении этого случая.
Идея барицентрических координат.
|
|
Выберем на плоскости произвольный треугольник АВС (рис. 8), который в дальнейшем назовем координатным, или базисным треугольником Мебиуса. Пусть р¹0 и (Р, р) ¾ произвольная материальная точка, лежащая в плоскости этого треугольника. Тогда возможно подобрать для точек А, В, С такие массы а, b, с (не обязательно положительные), чтобы объединением трех материальных точек (А, а), (В, b) и (С, с) служила точка (Р, р). Это можно себе представить следующим образом.
Ясно, что не может быть одновременно РА½½ ВС, РВ½½ СА, РС½½ АВ. Пусть, для определённости, РА и ВС не параллельны. Соединим Р с А и отметим точку А1, в которой АР встречает прямую ВС. Подберём три действительных числа а, b, c так, чтобы
b×BA1 = c×A1C,
a×AP = (b + c)×PA1,
a + b + c = p.
Это всегда возможно сделать. Тогда
(P, p) = (A, a) + (B, b) + (C, c).
Обратно, если возьмём три произвольных действительных числа a, b, c, причём a + b + c ¹ 0, то существует вполне определённая материальная точка (Р, р) такая, что (Р, р) = (A, a) + (B, b) + (C, c).
Таким образом, каждую материальную точку Рº(Р, р) на плоскости можно вполне охарактеризовать тремя числами, а именно тремя массами a, b и с, которые надо поместить в вершинах базисного треугольника, чтобы точка Р оказалась объединением трёх образующихся при этом материальных точек (A, a), (B, b) и (C, c). Эти три числа называют барицентрическими координатами материальной точки Р («барицентр» означает «центр тяжести»): а — первая барицентрическая координата, b — вторая, с — третья. Понятно, что те же три числа a, b, c определяют также положение носителя материальной точки Р. Поэтому эти три числа называют также барицентрическими координатами (геометрической) точки Р.
Таким образом, выражение «барицентрическими координатами точки Р служат числа a, b, c» означает только то, что имеет место равенство
(A, a) + (B, b) + (C, c) = (P, p),
где
p = a + b + c.
Если массы трёх материальных точек увеличить (или уменьшить) в одно и то же число раз, то от этого положение их центра тяжести не изменится. Поэтому барицентрическими координатами геометрической точки Р будут также числа k×a, k×b, k×c, где k — любое действительное число, не равное нулю.
Итак, геометрическая точка Р (в отличие от материальной точки Р) имеет бесконечно много троек барицентрических координат, причём каждая из этих троек может быть получена из какой-либо одной тройки (a, b, c) путём умножения на какую-либо константу k, отличную от нуля.
Если точка Р находится внутри координатного треугольника, то все три её барицентрические координаты одного знака (их можно считать положительными). Если точка Р — на какой-либо стороне координатного треугольника или на её продолжении, то хотя бы одна барицентрическая координата этой точки равна нулю. В остальных случаях две координаты точки Р — одного знака, а третья имеет противоположный знак.
Если точка Р расположена внутри базисного треугольника ABC, то в качестве её барицентрических координат можно принять площади треугольников BPC, CPA и APB.
Применение барицентрических координат позволяет внести одно существенное упрощение в рассуждения, связанное с рассмотрением материальных точек : рассмотрение любых произвольно расположенных материальных точек в любом числе сводится к рассмотрению только таких материальных точек, которые имеют носителями вершины базисного треугольника.
Правильные многогранники
Платону принадлежит разработка некоторых важных методологических проблем математического познания: аксиоматическое построение математики, исследование отношений между математическими методами и диалектикой, анализ основных форм математического знания. Так, процесс доказательства необходимо связывает набор доказанных положений в систему, в основе которой лежат некоторые недоказуемые положения. Тот факт, что начала математических наук "суть предположения", может вызвать сомнение в истинности всех последующих построений. Платон считал такое сомнение необоснованным. Согласно его объяснению, хотя сами математические науки, "пользуясь предположениями, оставляют их в неподвижности и не могут дать для них основания", предположения находят основания посредством диалектики. Платон высказал и ряд других положений, оказавшихся плодотворными для развития математики. Так, в диалоге "Пир" выдвигается понятие предела; идея выступает здесь как предел становления вещи.
ТЕЛА ПЛАТОНА.
Тела Платона-это выпуклые многогранники, все грани которых правильные многоугольники. Все многогранные углы правильного многогранника конгруэнтны. Как это следует уже из подсчета суммы плоских углов при вершине, выпуклых правильных многогранников не больше пяти. Указанным ниже путем можно доказать, что существует именно пять правильных многогранников (это доказал Евклид). Они - правильный тетраэдр, куб, октаэдр, додекаэдр и икосаэдр.
ТАБЛИЦА№1
|
Название: |
Число ребер при вершине |
Число сторон грани |
Число граней |
Число ребер |
Число вершин |
|
Тетраэдр |
3 |
3 |
4 |
6 |
4 |
|
Куб |
3 |
4 |
6 |
12 |
8 |
|
Октаэдр |
4 |
3 |
8 |
12 |
6 |
|
Додекаэдр |
3 |
5 |
12 |
30 |
20 |
|
Икосаэдр |
5 |
3 |
20 |
30 |
12 |
ТАБЛИЦА№2
|
Название: |
Радиус описанной сферы |
Радиус вписанной сферы |
Объем |
|
Тетраэдр |
а\/6 4 |
a\/6 12 |
a3\/2 12 |
|
Куб |
а\/3 2 |
a 2 |
a3 |
|
Октаэдр |
а\/2 2 |
a\/6 6 |
a3\/2 12 |
|
Додекаэдр |
a 4 \/18+6\/5 |
1 2 25+11\/5 10 |
a3 4 (15+7\/5) |
|
Икосаэдр |
|
a 12(3+\/5)\/3 |
5 12 a3(3+\/5) |
Тетраэдр-четырехгранник, все грани которого треугольники, т.е. треугольная пирамида; правильный тетраэдр ограничен четырьмя равносторонними треугольниками; один из пяти правильных многоугольников. (рис.1).
Куб или правильный гексаэдр - правильная четырехугольная призма с равными ребрами, ограниченная шестью квадратами. (рис.2).
Октаэдр-восьмигранник; тело, ограниченное восемью треугольниками; правильный октаэдр ограничен восемью равносторонними треугольниками; один из пяти правильных многогранников. (рис.3).
Додекаэдр-двенадцатигранник, тело, ограниченное двенадцатью многоугольниками; правильный пятиугольник; один из пяти правильных многогранников. (рис.4).
Икосаэдр-двадцатигранник, тело, ограниченное двадцатью многоугольниками; правильный икосаэдр ограничен двадцатью равносторонними треугольниками; один из пяти правильных многогранников. (рис.5).
Куб и октаэдр дуальны, т.е. получаются друг из друга, если центры тяжести граней одного принять за вершины другого и обратно. Аналогично дуальны додекаэдр и икосаэдр. Тетраэдр дуален сам себе. Правильный додекаэдр получается из куба построением «крыш» на его гранях (способ Евклида), вершинами тетраэдра являются любые четыре вершины куба, попарно не смежные по ребру. Так получаются из куба все остальные правильные многогранники. Сам факт существования всего пяти действительно правильных многогранников удивителен- ведь правильных многоугольников на плоскости бесконечно много!
Все правильные многогранники были известны еще в Древней Греции, и им посвящена заключительная, XII книга знаменитых начал Евклида. Эти многогранники часто называют также платоновыми телами в идеалистической картине мира, данной великим древнегреческим мыслителем Платоном. Четыре из них олицетворяли четыре стихии: тетраэдр-огонь, куб-землю, икосаэдр-воду и октаэдр-воздух; пятый же многогранник, додекаэдр, символизировал все мироздание его по латыни стали называть quinta essentia («пятая сущность»). Придумать правильный тетраэдр, куб, октаэдр, по-видимому, было не трудно, тем более что эти формы имеют природные кристаллы, например: куб-монокристалл поваренной соли (NaCl), октаэдр-монокристалл алюмокалиевых квасцов ((KalSO4)2*12H2O). Существует предположение, что форму додекаэдра древние греки получили, рассматривая кристаллы пирита (сернистого колчедана FeS). Имея же додекаэдр нетрудно построить и икосаэдр: его вершинами будут центры двенадцати граней додекаэдра.
Шпаргалка по тригонометрии
ARCSIN a
-p /2£ arcsin a £ p /2 sin(arcsin a)=a
arcsin (-a)= -arcsin a
|
a |
0 |
1/2 |
Ö 2/2 |
Ö 3/2 |
1 |
| arcsin a |
0 |
p /6 |
p /4 |
p /3 |
p /2 |
SIN X= A
x=(-1)n arcsin a +p k
|
sin x=0 |
x=p k |
|
sin x=1 |
x=p /2+2p k |
|
sin x=-1 |
x=-p /2+2p k |
ARCCOS a
0 £ arccos a £ p cos(arccos a)=a
arccos (-a)=p -arccos a
|
a |
0 |
1/2 |
Ö 2/2 |
Ö 3/2 |
1 |
| arccos a |
p /2 |
p /3 |
p /4 |
p /6 |
0 |
COS X= A
x=± arccos a +2p k
|
cos x=0 |
x=p /2+p k |
|
cos x=1 |
x=2p k |
|
cos x=-1 |
x=p +2p k |
ARCTG a
-p /2£ arctg a £ p /2 tg(arctg a)=a
arctg (-a)= -arctg a
|
a |
0 |
Ö 3/3 |
1 |
Ö 3 |
|
tg a |
0 |
p /6 |
p /4 |
p /3 |
TG X= A
x=± arctg a +p k
sina *cosb =1/2[sin(a -b )+sin(a +b )]
sina *sinb =1/2[cos(a -b )-cos(a +b )]
cosa *cosb =1/2[cos(a -b )+cos(a +b)]
sina *cosb =1/2[sin(a -b )+sin(a +b )]
sina *sinb =1/2[cos(a -b )-cos(a +b )]
cosa *cosb =1/2[cos(a -b )+cos(a +b)]
sina +sinb =2sin(a +b )/2 * cos(a -b )/2
sina -sinb =2sin(a -b )/2 * cos(a +b )/2
cosa +cosb =2cos(a +b )/2 * cos(a -b )/2
cosa -cosb =-2sin(a +b )/2 * sin(a -b )/2
(a+b)2=a2+2ab+b2
(a-b)2=a2+2ab+b2
(a+b+c)2=a2+b2+c2+2ab+2ac+2bc
a2-b2=(a-b)(a+b)
(a+b)3=a3+3a2b+3ab2+b3
(a-b)3=a3-3a2b+3ab2-b3
a3+b3=(a+b)(a2-ab+b2)
a3-b3=(a-b)(a2+ab+ b2)
| 0 | p /6 | p /4 | p /3 | p /2 | p | 2/3p | 3/4p | 5/6p | 3/2p | |
| 0 | 30° | 45° | 60° | 90° | 180 | 120° | 135° | 150° | 270° | |
| sin | 0 | 1/2 | Ö 2/2 | Ö 3/2 | 1 | 0 | Ö 3/2 | Ö 2/2 | 1/2 | -1 |
| cos | 1 | Ö 3/2 | Ö 2/2 | 1/2 | 0 | -1 | -1/2 | -Ö 2/2 | -Ö 3/2 | 0 |
| tg | 0 | 1/Ö 3 | 1 | Ö 3 | - | 0 | -Ö 3 | -1 | -1/Ö 3 | - |
| ctg | - | Ö 3 | 1 | 1/Ö 3 | 0 | - | -1/Ö 3 | -1 | -Ö 3 | 0 |
sin2+cos2=1 sin=±Ö 1-cos2 sin(-a )=-sina tg(-a )=-tga
tg• ctg=1 cos=±Ö 1-sin2 cos(-a )=cosa ctg(-g)=-ctga
tg=1/ctg ctg=1/tg 1+tg2=1/cos2=sec2
sin2=(1-cos)(1+cos) 1+ctg2=1/sin2=cosec2 sin2a =2sina • cosa
cos2=(1-sin)(1+sin) 1-tg2/(1+tg2)=cos4-sin4 cos2a =cos2 a -sin2 a
cos/(1-sin)=1+sin/cos 1/(tg+ctg)=sin• cos tg2a =2tga /1-tga
cos(a +b )=cosa • cosb -sina • sinb sin3a =3sina -4sin3a
cos(a -b )=cosa • cosb +sina • sinb cos3a =4cos3a -3cosa
sin(a +b )=sina • cosb +cosa • sinb tg(a +b )=tga +tgb
sin(a -b )=sina • cosb -cosa • sinb 1-tga • tgb
2cos2a /2=1+cosa 2sin2a /2=1-cosa
| 0 | p /6 | p /4 | p /3 | p /2 | p | 2/3p | 3/4p | 5/6p | 3/2p | |
| 0 | 30° | 45° | 60° | 90° | 180 | 120° | 135° | 150° | 270° | |
| sin | 0 | 1/2 | Ö 2/2 | Ö 3/2 | 1 | 0 | Ö 3/2 | Ö 2/2 | 1/2 | -1 |
| cos | 1 | Ö 3/2 | Ö 2/2 | 1/2 | 0 | -1 | -1/2 | -Ö 2/2 | -Ö 3/2 | 0 |
| tg | 0 | 1/Ö 3 | 1 | Ö 3 | - | 0 | -Ö 3 | -1 | -1/Ö 3 | - |
| ctg | - | Ö 3 | 1 | 1/Ö 3 | 0 | - | -1/Ö 3 | -1 | -Ö 3 | 0 |
sin2+cos2=1 sin=±Ö 1-cos2 sin(-a )=-sina tg(-a )=-tga
tg• ctg=1 cos=±Ö 1-sin2 cos(-a )=cosa ctg(-g)=-ctga
tg=1/ctg ctg=1/tg 1+tg2=1/cos2=sec2
sin2=(1-cos)(1+cos) 1+ctg2=1/sin2=cosec2 sin2a =2sina • cosa
cos2=(1-sin)(1+sin) 1-tg2/(1+tg2)=cos4-sin4 cos2a =cos2 a -sin2 a
cos/(1-sin)=1+sin/cos 1/(tg+ctg)=sin• cos tg2a =2tga /1-tga
cos(a +b )=cosa • cosb -sina • sinb sin3a =3sina -4sin3a
cos(a -b )=cosa • cosb +sina • sinb cos3a =4cos3a -3cosa
sin(a +b )=sina • cosb +cosa • sinb tg(a +b )=tga +tgb
sin(a -b )=sina • cosb -cosa • sinb 1-tga • tgb
sin(2p -a )=-sina sin(3p /2-a )=-cosa
cos(2p -a )=cosa cos(3p /2-a )=-sina
tg(2p -a )=-tga tg(3p /2-a )=ctga
sin(p -a )=sina ctg(3p /2-a )=tga
cos(p -a )=-cosa sin(3p /2+a )=-cosa
sin(p +a )=-sina cos(3p /2+a )=sina
cos(p +a )=-cosa tg(p /2+a )=-ctga
sin(p /2-a )=cosa ctg(p /2+a )=-tga
cos(p /2-a )=sina sina +sinb =2sin(a +b )/2cos(a -b )/2
tg(p /2-a )=ctga sina -sinb =2sin(a -b )/2*cos(a +b )/2
ctg(p /2-a )=tga cosa +cosb =2cos(a +b)/2cos(a -b )/2
sin(p /2+a )=cosa cosa -cosb =-2sin(a +b)/2sin(a -b )/2
cos(p /2+a )=-sina
Функция и её свойства
Функция- зависимость переменной у от переменной x, если каждому значению х соответствует единственное значение у.
Переменная х- независимая переменная или аргумент.
Переменная у- зависимая переменная
Значение функции- значение у, соответствующее заданному значению х.
Область определения функции- все значения, которые принимает независимая переменная.
Область значений функции (множество значений)- все значения, которые принимает функция.
Функция является четной- если для любого х из области определения функции выполняется равенство f(x)=f(-x)
Функция является нечетной- если для любого х из области определения функции выполняется равенство f(-x)=-f(x)
Возрастающая функция- если для любых х1 и х2, таких, что х1< х2, выполняется неравенство f(х1)<f(х2)
Убывающая функция- если для любых х1 и х2, таких, что х1< х2, выполняется неравенство f(х1)>f(х2)
Способы задания функции
¨ Чтобы задать функцию, нужно указать способ, с помощью которого для каждого значения аргумента можно найти соответствующее значение функции. Наиболее употребительным является способ задания функции с помощью формулы у=f(x), где f(x)-íåêîòîðîå âыðàæåíèå с переменной х. В таком случае говорят, что функция задана формулой или что функция задана аналитически.
¨ На практике часто используется табличный способ задания функции. При этом способе приводится таблица, указывающая значения функции для имеющихся в таблице значений аргумента. Примерами табличного задания функции являются таблица квадратов, таблица кубов.
Виды функций и их свойства
1) Постоянная функция- функция, заданная формулой у=b, где b-некоторое число. Графиком постоянной функции у=b является прямая, параллельная оси абсцисс и проходящая через точку (0;b) на оси ординат
2) Прямая пропорциональность- функция, заданная формулой у=kx, где к¹0. Число k называется коэффициентом пропорциональности.
Cвойства функции y=kx:
1. Область определения функции- множество всех действительных чисел
2. y=kx - нечетная функция
3. При k>0 функция возрастает, а при k<0 убывает на всей числовой прямой
3)Линейная функция- функция, которая задана формулой y=kx+b, где k и b-действительные числа. Если в частности, k=0, то получаем постоянную функцию y=b; если b=0, то получаем прямую пропорциональность y=kx.
Свойства функции y=kx+b:
1. Область определения- множество всех действительных чисел
2. Функция y=kx+b общего вида, т.е. ни чётна, ни нечётна.
3. При k>0 функция возрастает, а при k<0 убывает на всей числовой прямой
Графиком функции является прямая.
4)Обратная пропорциональность- функция, заданная формулой y=k/х, где k¹0 Число k называют коэффициентом обратной пропорциональности.
Свойства функции y=k/x:
1. Область определения- множество всех действительных чисел кроме нуля
2. y=k/x- нечетная функция
3. Если k>0, то функция убывает на промежутке (0;+¥) и на промежутке (-¥;0). Если k<0, то функция возрастает на промежутке (-¥;0) и на промежутке (0;+¥).
Графиком функции является гипербола.
5)Функция y=x2
Свойства функции y=x2:
1. Область определения- вся числовая прямая
2. y=x2 - четная функция
3. На промежутке [0;+¥) функция возрастает
4. На промежутке (-¥;0] функция убывает
Графиком функции является парабола.
6)Функция y=x3
Свойства функции y=x3:
1. Область определения- вся числовая прямая
2. y=x3 -нечетная функция
3. Функция возрастает на всей числовой прямой
Графиком функции является кубическая парабола
7)Степенная функция с натуральным показателем- функция, заданная формулой y=xn, где n- натуральное число. При n=1 получаем функцию y=x, ее свойства рассмотрены в п.2. При n=2;3 получаем функции y=x2; y=x3. Их свойства рассмотрены выше.
Пусть n- произвольное четное число, большее двух: 4,6,8... В этом случае функция y=xn обладает теми же свойствами, что и функция y=x2. График функции напоминает параболу y=x2, только ветви графика при |х|>1 тем круче идут вверх, чем больше n, а при |х|<1 тем «теснее прижимаются» к оси Х, чем больше n.
Пусть n- произвольное нечетное число, большее трех: 5,7,9... В этом случае функция y=xn обладает теми же свойствами, что и функция y=x3. График функции напоминает кубическую параболу.
8)Степенная функция с целым отрицательным показателем- функция, заданная формулой y=x-n, где n- натуральное число. При n=1 получаем y=1/х, свойства этой функции рассмотрены в п.4.
Пусть n- нечетное число, большее единицы: 3,5,7... В этом случае функция y=x-n обладает в основном теми же свойствами, что и функция y=1/х.
Пусть n- четное число, например n=2.
Свойства функции y=x-2:
1. Функция определена при всех x¹0
2. y=x-2 - четная функция
3. Функция убывает на (0;+¥) и возрастает на (-¥;0).
Теми же свойствами обладают любые функции при четном n, большем двух.
9)Функция y=Öх
Свойства функции y=Öх:
1. Область определения - луч [0;+¥).
2. Функция y=Öх - общего вида
3. Функция возрастает на луче [0;+¥).
10)Функция y=3Öх
Свойства функции y=3Öх:
1. Область определения- вся числовая прямая
2. Функция y=3Öх нечетна.
3. Функция возрастает на всей числовой прямой.
11)Функция y=nÖх
При четном n функция обладает теми же свойствами, что и функция y=Öх. При нечетном n функция y=nÖх обладает теми же свойствами, что и функция y=3Öх.
12)Степенная функция с положительным дробным показателем- функция, заданная формулой y=xr, где r- положительная несократимая дробь.
Свойства функции y=xr:
1. Область определения- луч [0;+¥).
2. Функция общего вида
3. Функция возрастает на [0;+¥).
На рисунке изображен график функции y=x5/2. Он заключен между графиками функций y=x2 и y=x3, заданных на промежутке [0;+¥).Подобный вид имеет любой график функции вида y=xr, где r>1.
На рисунке изображен график функции y=x2/3. Подобный вид имеет график любой степенной функции y=xr , где 0<r<1
13)Степенная функция с отрицательным дробным показателем-функция, заданная формулой y=x-r, где r- положительная несократимая дробь.
Свойства функции y=x-r:
1. Обл. определения -промежуток (0;+¥)
2. Функция общего вида
3. Функция убывает на (0;+¥)
14)Обратная функция
Если функция y=f(x) такова, что для любого ее значения yo уравнение f(x)=yo имеет относительно х единственный корень, то говорят, что функция f обратима.
Если функция y=f(x) определена и возрастает (убывает) на промежутке Х и областью ее значений является промежуток Y, то у нее существует обратная функция, причем обратная функция определена и возрастает(убывает) на Y.
Таким образом, чтобы построить график функции, обратной к функции y=f(x), надо график функции y=f(x) подвергнуть преобразованию симметрии относительно прямой y=x.
15)Сложная функция- функция, аргументом которой является другая любая функция.
Возьмем, к примеру, функцию y=x+4. Подставим в аргумент функцию y=x+2. Получается: y(x+2)=x+2+4=x+6. Это и будет являться сложной функцией.
Теорема Пифагора
Трудно найти человека, у которого имя Пифагора не ассоциировалось бы с теоремой Пифагора. Пожалуй, даже те, кто в своей жизни навсегда распрощался с математикой, сохраняют воспоминания о «пифагоровых штанах» — квадрате на гипотенузе, равновеликом двум квадратам на катетах. Причина такой популярности теоремы Пифагора триедина: это простота — красота — значимость. В самом деле, теорема Пифагора проста, но не очевидна. Это сочетание двух противоречивых начал и придает ей особую притягательную силу, делает ее красивой. Но, кроме того, теорема Пифагора имеет огромное значение: она применяется в геометрии буквально на каждом шагу, и тот факт, что существует около 500 различных доказательств этой теоремы (геометрических, алгебраических, механических и т.д.), свидетельствует о гигантском числе ее конкретных реализаций. Открытие теоремы Пифагором окружено ореолом красивых легенд. Прокл, комментируя последнее предложение первой книги «Начал» Евклида, пишет: «Если послушать тех, кто любит повторять древние легенды, то придется сказать, что эта теорема восходит к Пифагору; рассказывают, что он в честь этого открытия принес в жертву быка». Впрочем, более щедрые сказители одного быка превратили в одну гекатомбу, а это уже целая сотня. И хотя еще Цицерон заметил, что всякое пролитие крови было чуждо уставу пифагорейского ордена, легенда эта прочно срослась с теоремой Пифагора и через две тысячи лет продолжала вызывать горячие отклики. Так, оптимист Михаил Ломоносов (1711--1765) писал: «Пифагор за изобретение одного геометрического правила Зевсу принес на жертву сто волов. Но ежели бы за найденные в нынешние времена от остроумных математиков правила по суеверной его ревности поступать, то едва бы в целом свете столько рогатого скота сыскалось». А вот ироничный Генрих Гейне (1797—1856) видел развитие той же ситуации несколько иначе: «Кто знает! Кто знает! Возможно, душа Пифагора переселилась в беднягу кандидата, который не смог доказать теорему Пифагора и провалился из-за этого на экзаменах, тогда как в его экзаменаторах обитают души тех быков, которых Пифагор, обрадованный открытием своей теоремы, принес в жертву бессмертным богам». Сегодня теорема Пифагора обнаружена в различных частных задачах и чертежах: и в египетском треугольнике в папирусе времен фараона Аменемхета первого (ок. 2000 до н.э.), и в вавилонских клинописных табличках эпохи царя Хаммурапи (XVIII в. до н.э.), и в древнеиндийском геометрическо-теологическом трактате VII —V вв. до н.э. «Сульва сутра» («Правила веревки»). В древнейшем китайском трактате «Чжоу-би суань цзинь», время создания которого точно не известно, утверждается, что в XII в. до н. э. китайцы знали свойства египетского треугольника, а к VI в. до н.э.—и общий вид теоремы. Несмотря на все это, имя Пифагора столь прочно сплавилось с теоремой Пифагора, что сейчас просто невозможно представить, что это словосочетание распадется. То же относится и к легенде о заклании быков Пифагором. Да и вряд ли нужно препарировать историко-математическим скальпелем красивые древние предания. Сегодня принято считать, что Пифагор дал первое доказательство носящей его имя теоремы. Увы, от этого доказательства также не сохранилось никаких следов.
Я рассмотрю некоторые классические доказательства теоремы Пифагора, известные из древних трактатов. Сделать это полезно еще и потому, что в современных школьных учебниках дается алгебраическое доказательство теоремы. При этом бесследно исчезает первозданная геометрическая аура теоремы, теряется та нить Ариадны, которая вела древних мудрецов к истине, а путь этот почти всегда оказывался кратчайшим и всегда красивым. Итак, Теорема Пифагора.
Б иография
Пифагора.
Великий ученый Пифагор родился около 570 г. до н.э. на острове Самосе. Отцом
Пифагора был Мнесарх, резчик по драгоценным камням. Имя же матери Пифагора
не известно. По многим античным свидетельствам, родившийся мальчик был
сказочно красив, а вскоре проявил и свои незаурядные способности. Среди
учителей юного Пифагора традиция называет имена старца Гермодаманта и
Ферекида Сиросского (хотя и нет твердой уверенности в том, что именно
Гермодамант и Ферекид были первыми учителями Пифагора). Целые дни
проводил юный Пифагор у ног старца Гермодаманта, внимая мелодии
кифары и гекзаметрам Гомера. Страсть к музыке и поэзии великого Гомера
Пифагор сохранил на всю жизнь. И, будучи признанным мудрецом, окруженным
толпой учеников, Пифагор начинал день с пения одной из песен Гомера. Ферекид
же был философом и считался основателем италийской школы философии. Таким
образом, если Гермодамант ввел юного Пифагора в круг муз, то Ферекид обратил
его ум к логосу. Ферекид направил взор Пифагора к природе и в ней одной
советовал видеть своего первого и главного учителя. Но как бы то ни было,
неугомонному воображению юного Пифагора очень скоро стало тесно на
маленьком Самосе, и он отправляется в Милет, где встречается с другим ученым
- Фалесом. Фалес советует ему отправится за знаниями в Египет, что Пифагор и
сделал.
иография
Пифагора.
Великий ученый Пифагор родился около 570 г. до н.э. на острове Самосе. Отцом
Пифагора был Мнесарх, резчик по драгоценным камням. Имя же матери Пифагора
не известно. По многим античным свидетельствам, родившийся мальчик был
сказочно красив, а вскоре проявил и свои незаурядные способности. Среди
учителей юного Пифагора традиция называет имена старца Гермодаманта и
Ферекида Сиросского (хотя и нет твердой уверенности в том, что именно
Гермодамант и Ферекид были первыми учителями Пифагора). Целые дни
проводил юный Пифагор у ног старца Гермодаманта, внимая мелодии
кифары и гекзаметрам Гомера. Страсть к музыке и поэзии великого Гомера
Пифагор сохранил на всю жизнь. И, будучи признанным мудрецом, окруженным
толпой учеников, Пифагор начинал день с пения одной из песен Гомера. Ферекид
же был философом и считался основателем италийской школы философии. Таким
образом, если Гермодамант ввел юного Пифагора в круг муз, то Ферекид обратил
его ум к логосу. Ферекид направил взор Пифагора к природе и в ней одной
советовал видеть своего первого и главного учителя. Но как бы то ни было,
неугомонному воображению юного Пифагора очень скоро стало тесно на
маленьком Самосе, и он отправляется в Милет, где встречается с другим ученым
- Фалесом. Фалес советует ему отправится за знаниями в Египет, что Пифагор и
сделал.
В 548 г. до н.э. Пифагор прибыл в Навкратис – самосскую колонию, где было у кого найти кров и пищу. Изучив язык и религию египтян, он уезжает в Мемфис. Несмотря на рекомендательное письмо фараона, хитроумные жрецы не спешили раскрывать Пифагору свои тайны, предлагая ему сложные испытания. Но влекомый жаждой к знаниям, Пифагор преодолел их все, хотя по данным раскопок египетские жрецы не многому могли его научить, т.к. в то время египетская геометрия была чисто прикладной наукой (удовлетворявшей потребность того времени в счете и в измерении земельных участков). Поэтому, научившись всему, что дали ему жрецы, он, убежав от них, двинулся на родину в Элладу. Однако, проделав часть пути, Пифагор решается на сухопутное путешествие, во время которого его захватил в плен Камбиз, царь Вавилона, направлявшийся домой. Не стоит драматизировать жизнь Пифагора в Вавилоне, т.к. великий властитель Кир был терпим ко всем пленникам. Вавилонская математика была, бесспорно, более развитой (примером этому может служить позиционная система исчисления), чем египетская, и Пифагору было чему поучится. Но в 530 г. до н.э. Кир двинулся в поход против племен в Средней Азии. И, пользуясь переполохом в городе, Пифагор сбежал на родину. А на Самосе в то время царствовал тиран Поликрат. Конечно же, Пифагора не устраивала жизнь придворного полу раба, и он удалился в пещеры в окрестностях Самоса. После нескольких месяцев притязаний со стороны Поликрата, Пифагор переселяется в Кротон. В Кротоне Пифагор учредил нечто вроде религиозно-этического братства или тайного монашеского ордена («пифагорейцы»), члены которого обязывались вести так называемый пифагорейский образ жизни. Это был одновременно и религиозный союз, и политический клуб, и научное общество. Надо сказать, что некоторые из проповедуемых Пифагором принцыпов достойны подражания и сейчас.
...Прошло 20 лет. Слава о братстве разнеслась по всему миру. Однажды к Пифагору приходит Килон, человек богатый, но злой, желая спьяну вступить в братство. Получив отказ, Килон начинает борьбу с Пифагором, воспользовавшись поджогом его дома. При пожаре пифагорейцы спасли жизнь своему учителю ценой своей, после чего Пифагор затосковал и вскоре покончил жизнь самоубийством.
![]()
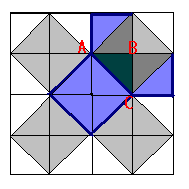 "Квадрат,
построенный на гипотенузе прямоугольного треугольника, равновелик сумме
квадратов, построенных на его катетах." Простейшее
доказательство
теоремы получается в простейшем случае равнобедренного прямоугольного
треугольника. Вероятно, с него и начиналась теорема. В самом деле,
достаточно просто посмотреть на мозаику равнобедренных прямоугольных
треугольников (рис. 1), чтобы убедиться в справедливости теоремы. Например,
для
ÙABC
: квадрат,
построенный на гипотенузе АС, содержит 4 исходных треугольника, а
квадраты, построенные на катетах,— по два. Теорема доказана.
"Квадрат,
построенный на гипотенузе прямоугольного треугольника, равновелик сумме
квадратов, построенных на его катетах." Простейшее
доказательство
теоремы получается в простейшем случае равнобедренного прямоугольного
треугольника. Вероятно, с него и начиналась теорема. В самом деле,
достаточно просто посмотреть на мозаику равнобедренных прямоугольных
треугольников (рис. 1), чтобы убедиться в справедливости теоремы. Например,
для
ÙABC
: квадрат,
построенный на гипотенузе АС, содержит 4 исходных треугольника, а
квадраты, построенные на катетах,— по два. Теорема доказана.
Рис. 2
 Древнекитайское
доказательство.
Математические трактаты Древнего Китая дошли
до нас в редакции II в. до н.э. Дело в том, что в 213 г. до н.э. китайский
император Ши Хуан-ди,
стремясь ликвидировать прежние традиции, приказал
сжечь все древние книги. Во II в. до н.э. в
Китае была изобретена бумага и одновременно
начинается воссоздание древних книг. Так возникла тематика в девяти книгах»
— главное из сохранившихся математико
- астрономических сочинений
в книге «Математики»
помещен чертеж
(рис. 2, а), доказывающий
теорему Пифагора. Ключ к этому доказательству
Древнекитайское
доказательство.
Математические трактаты Древнего Китая дошли
до нас в редакции II в. до н.э. Дело в том, что в 213 г. до н.э. китайский
император Ши Хуан-ди,
стремясь ликвидировать прежние традиции, приказал
сжечь все древние книги. Во II в. до н.э. в
Китае была изобретена бумага и одновременно
начинается воссоздание древних книг. Так возникла тематика в девяти книгах»
— главное из сохранившихся математико
- астрономических сочинений
в книге «Математики»
помещен чертеж
(рис. 2, а), доказывающий
теорему Пифагора. Ключ к этому доказательству
Рис. 2
подобрать нетрудно. В самом деле, на древнекитайском чертеже четыре равных прямоугольных треугольника с катетами а, b и гипотенузой с уложены так, что их внешний контур образует квадрат со стороной а+b, а внутренний — квадрат со стороной с, построенный на гипотенузе (рис. 2, б). Если квадрат со стороной с вырезать и оставшиеся 4 затушеванных треугольника уложить в два прямоугольника (рис. 2, в), то ясно, что образовавшаяся пустота, с одной стороны, равна с2, а с другой — а2+Ь2, т.е. с2=а2+Ь2. Теорема доказана. Заметим, что при таком доказательстве построения внутри квадрата на гипотенузе, которые мы видим на древнекитайском чертеже (рис. 2, а), не используются. По-видимому, древнекитайские математики имели другое доказательство. Именно если в квадрате со стороной с два заштрихованных треугольника (рис. 2, б) отрезать и приложить гипотенузами к двум другим гипотенузам (рис. 2, г), то легко обнаружить, что полученная фигура, которую иногда называют «креслом невесты», состоит из двух квадратов со сторонами а и b, т.е. с2=а2+Ь2.

Рис. 3
На рисунке 3 воспроизведен чертеж из трактата «Чжоу-би...». Здесь теорема Пифагора рассмотрена для египетского треугольника с катетами 3, 4 и гипотенузой 5 единиц измерения. Квадрат на гипотенузе содержит 25 клеток, а вписанный в него квадрат на большем катете—16. Ясно, что оставшаяся часть содержит 9 клеток. Это и будет квадрат на меньшем катете.

Рис. 4
Древнеиндийское доказательство. Математики Древней Индии заметили, что для доказательства теоремы Пифагора достаточно использовать внутреннюю часть древнекитайского чертежа. В написанном на пальмовых листьях трактате «Сиддханта широмани» («Венец знания») крупнейшего индийского математика XII в. Бхаскары помещен чертеж (рис. 4, а) с характерным для индийских доказательств словом «смотри!». Как видим, прямо-угольньные треугольники уложены здесь гипотенузой наружу и квадрат с2 перекладывается в «кресло невесты» а2-b2 (рис. 4, б). Заметим, что частные случаи теоремы Пифагора (например, построение квадрата, площадь которого вдвое больше площади данного квадрата) встречаются в древнеиндийском трактате «Сульва сутра» (VII —V вв. до н.э.).
![]()
Доказательство
Евклида
приведено в предложении 47 первой книги «Начал». На гипотенузе и катетах
прямоугольного треугольника АВС
строятся соответствующие квадраты (рис. 5) и доказывается, что
прямоугольник BJLD
равновелик квадрату ABFH,
а прямоугольник
ICEL
— квадрату
АС КС. Тогда сумма квадратов на катетах будет равна квадрату на
гипотенузе. В самом деле, затушеванные на рисунке треугольники
ABD и BFC
равны по двум сторонам и углу между ними:
FB=AB,
BC==BD и
ÐFBC=d+ÐABC=ÐABD.
Но
SABD=1/2 SBJLD,
так как у треугольника ABD и прямоугольника
BJLD общее основание BD и общая
высота LD. Аналогично
SFBC=1\2
SABFH (BF—общее
основание, АВ—общая
 высота).
Отсюда, учиты
высота).
Отсюда, учиты
Рис. 5
вая, что SABD=SFBC , имеем SBJLD= SABFH. Аналогично, используя равенство треугольников ВСК. и АСЕ, доказывается, что SJCEL=SACKG. Итак, SABFH+SACKG=SBJLD+SJCEL= SBCED , что и требовалось доказать. Доказательство Евклида в сравнении с древнекитайским или древнеиндийским выглядит чрезмерно сложным. По этой причине его нередко называли «ходульным» и «надуманным». Но такое мнение поверхностно. Теорема Пифагора у Евклида является заключительным звеном в цепи предложений 1-й книги «Начал». Для того чтобы логически безупречно построить эту цепь, чтобы каждый шаг доказательства был основан на ранее доказанных предложениях, Евклиду нужен был именно выбранный им путь.
Еще давно была изобретена головоломка, называемая сегодня «Пифагор». Нетрудно убедиться в том, что в основе семи частей головоломки лежат равнобедренный прямоугольный треугольник и квадраты, построенные на его катетах, или, иначе, фигуры, составленные из 16 одинаковых равнобедренных прямоугольных треугольников и потому укладывающиеся в квадрат. Такова лишь малая толика богатств, скрытых в жемчужине античной математики — теореме Пифагора. Далее я рассмотрю несколько алгебраических доказательств теоремы.
ДОКАЗАТЕЛЬСТВО ТЕОРЕМЫ ПИФАГОРА. Пусть Т— прямоугольный треугольник с катетами а, b и гипотенузой с (рис. 6, а). Докажем, что с2=а2+Ь2.
Построим квадрат Q со стороной а+Ь (рис. 6, б). На сторонах квадрата Q возьмем точки А, В, С, D так, чтобы отрезки АВ, ВС, CD, DA отсекали от квадрата Q прямоугольные треугольники Т1, Т2, Т3, Т4 с катетами а и b. Четырехугольник ABCD обозначим буквой Р. Покажем, что Р — квадрат со стороной с.
Все треугольники Т1, Т2, Т3, Т4 равны треугольнику Т (по двум катетам). Поэтому их гипотенузы равны гипотенузе треугольника Т, т. е. отрезку с. Докажем, что все углы этого четырехугольника прямые.
Пусть a и b— величины острых углов треугольника Т. Тогда, как вам известно, a+b= 90°. Угол у при вершине А четырехугольника Р вместе с углами, равными a и b, составляет развернутый угол. Поэтому a+b=180°. И так как a+b= 90°, то g=90°. Точно так же доказывается, что и остальные углы четырехугольника Р прямые. Следовательно, четырехугольник Р — квадрат со стороной с.
Квадрат Q со стороной а+Ь слагается из квадрата Р со стороной с и четырех треугольников, равных треугольнику Т. Поэтому для их площадей выполняется равенство S(Q)=S(P)+4S(T) .
Так как S(Q)=(a+b) 2 ; S(P)=c2 и S(T)=1/2(ab), то, подставляя эти выражения в S(Q)=S(P)+4S(T), получаем равенство
(a+b) 2=c2+4*(1/2)ab . Поскольку (a+b)2=a2+b2+2ab, то равенство (a+b)2=c2+4*(1/2)ab можно записать так: a2+b2+2ab=c2+2ab.
Из равенства a2+b2+2ab=c2+2ab следует, что с2=а2+Ь2.
Ч.Т.Д.
ЕЩЕ ОДНО АЛГЕБРАИЧЕСКОЕ ДОКАЗАТЕЛЬСТВО.
Пусть АВС — данный прямоугольный треугольник с прямым углом С. Проведем высоту CD из вершины прямого угла С (рис. 7).
 По
определению косинуса угла
(Косинусом
острого угла прямоугольного треугольника называется отношение прилежащего
катета к гипотенузе)
соsА=AD/AC=AC/AB.
Отсюда
AB*AD=AC2.
Аналогично соsВ=BD/BC=BC/AB.
Отсюда
AB*BD=ВС2.
Складывая полученные равенства почленно и замечая, что
AD+DB=AB,
получим:
По
определению косинуса угла
(Косинусом
острого угла прямоугольного треугольника называется отношение прилежащего
катета к гипотенузе)
соsА=AD/AC=AC/AB.
Отсюда
AB*AD=AC2.
Аналогично соsВ=BD/BC=BC/AB.
Отсюда
AB*BD=ВС2.
Складывая полученные равенства почленно и замечая, что
AD+DB=AB,
получим:
АС2+ВС2=АВ(AD + DB)=АВ2. Теорема доказана.
В заключении еще раз хочется сказать о важности теоремы. Значение ее состоит прежде всего в том, что из нее или с ее помощью можно вывести большинство теорем геометрии. К сожалению, невозможно здесь привести все или даже самые красивые доказательства теоремы, однако хочется надеется, что приведенные примеры убедительно свидетельствуют об огромном интересе сегодня, да и вчера, проявляемом по отношению к ней.

